RMSD y RMSF

Carga de la tryectoria total

Bien, ahora podemos comenzar con el análisis de la trayectoria. Si bien, en general debemos enfocarnos en la fase de producción, para este ejemplo comenzaremos observando la evolución conformacional de la proteína a través de todas las fases de la trayectoria. Comenzamos cargando las librerías y archivos necesarios:

## pytraj.Trajectory, 5348 frames: 
## Size: 0.036339 (GB)
## <Topology: 304 atoms, 20 residues, 1 mols, non-PBC>
##

Cálculo del RMSD

Ahora procederemos a calcular el rmsd de todos los frames de la trayectoria con respecto a una estructura de referencia, que en este caso será la estructura lineal de la proteína; correspondiente al archivo tc5b_wb.pdb.

Ahora calculamos el RMSD de toda la trayectoria usando lineal_strc como estructura de referencia:

Grafica de RMSD

Para graficar el RMSD importamos las librerías matplotlib y seaborn y establecemos algunos parámetros por default para las gráficas.

Ahora generamos la gráfica de la trayectoria total:

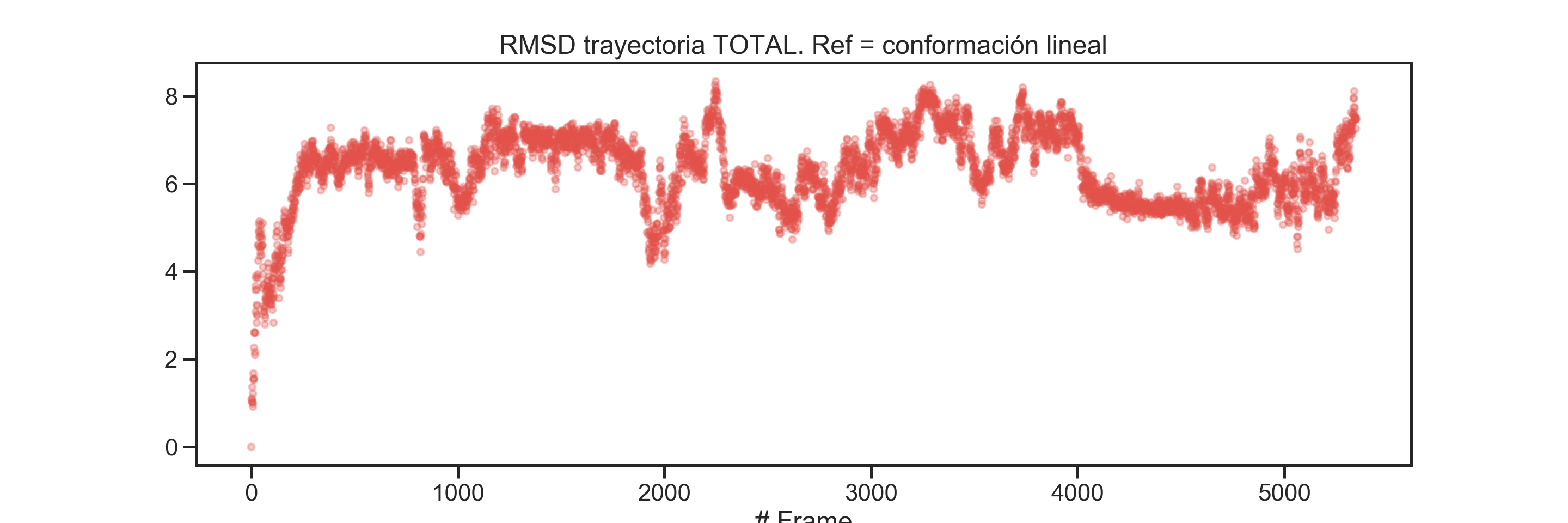
Como es de esperarse, conforme el tiempo de simulación avanza hay un aumento en el RMSD de cada frame con respecto a la conformación inicial.
Ahora bien, para un análisis más interesante usaremos como referencia la estructura por NMR de la proteína, con el objetivo de saber si, a lo largo de la simulación, las estructura de la proteína se aproxima a la estructura experimental.
Para ello cargamos la estructura NMR de la proteína.

Calculamos el RMSD de la trayectoria usando como referencia a nmr_strc. Seguido de ello, generamos la gráfica.

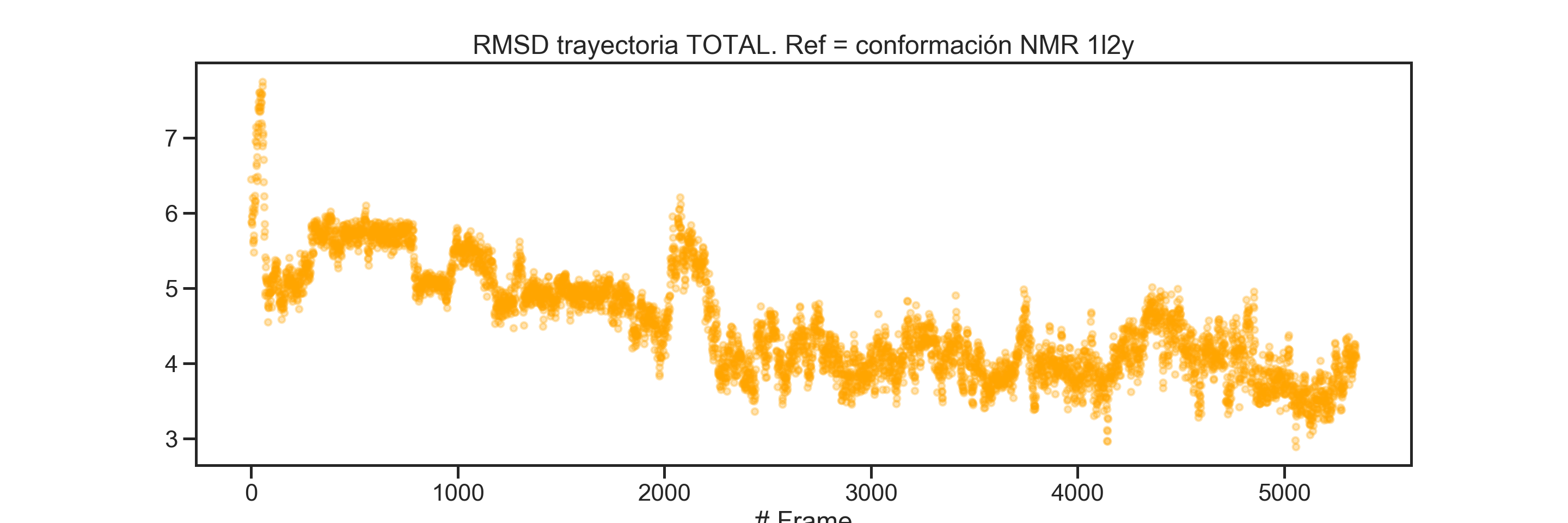
Como ves, al principio de la simulación la conformación inicial y la estructura por NMR son muy distintas (entre 6 a 8 A), sin embargo, a lo largo de la dinámica y sobre todo en la producción, la conformación de la porteína tiende a ser más parecida a la estructura NMR.

Finalmente, visualicemos únicamente la fase de producción con ambas referencias:

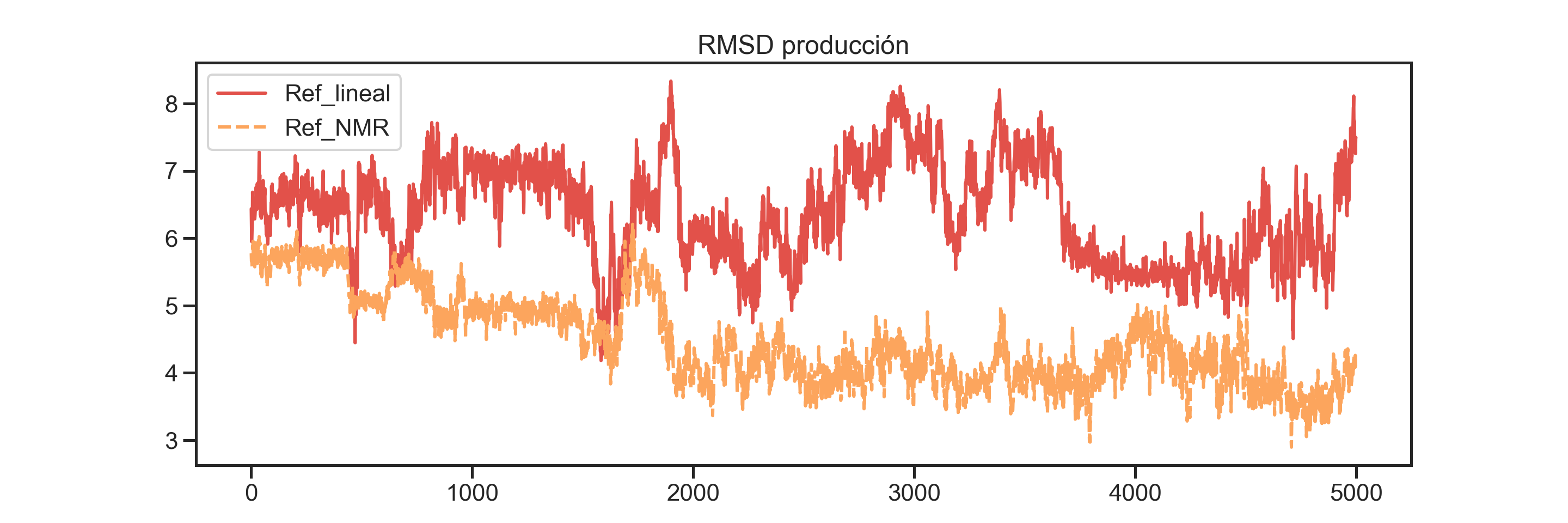
Cálculo del RMSF

Vamos a finalizar este análisis evaluando el RMSF de la proteína a lo largo de la fase de producción. Carguemos primero dicha trayectoria (Aunque bien podriamos usar los últimos frames del objeto full_traj).

Un pequeño paréntesis:

¿Es full_traj[:-5000] igual a prod_traj?
Es decir, ¿los últimos 5000 frames del objeto full_traj son iguales a todos frames de prod_traj?

## pytraj.Trajectory, 5000 frames: 
## Size: 0.033975 (GB)
## <Topology: 304 atoms, 20 residues, 1 mols, non-PBC>
## 
## pytraj.Trajectory, 5000 frames: 
## Size: 0.033975 (GB)
## <Topology: 304 atoms, 20 residues, 1 mols, non-PBC>
## 
## False

Si bien ambos objetos, , tienen la misma información, python nos dice que prod_traj == full_traj[-5000:] son distintos (False). Esto se debe a que las variables por referencia prod_traj y full_traj apuntan a objetos distintos en memoria, pero esto no significa que ambos objetos puedan tener información similar. Esto es importante y lo debemos de tener en cuenta al momento de querer copiar o manipular secciones de trayectorias. Finálicemos este paréntesis con el siguiente código:

## True
## False

Obtención del frame promedio y superposición de la trayectoria

Ahora volvamos al ejercicio para proceder a superponer toda la trayectoria a un frame promedio.

## pytraj.Trajectory, 5000 frames: 
## Size: 0.033975 (GB)
## <Topology: 304 atoms, 20 residues, 1 mols, non-PBC>
##

Ahora calculamos el RMSF de toda la producción:

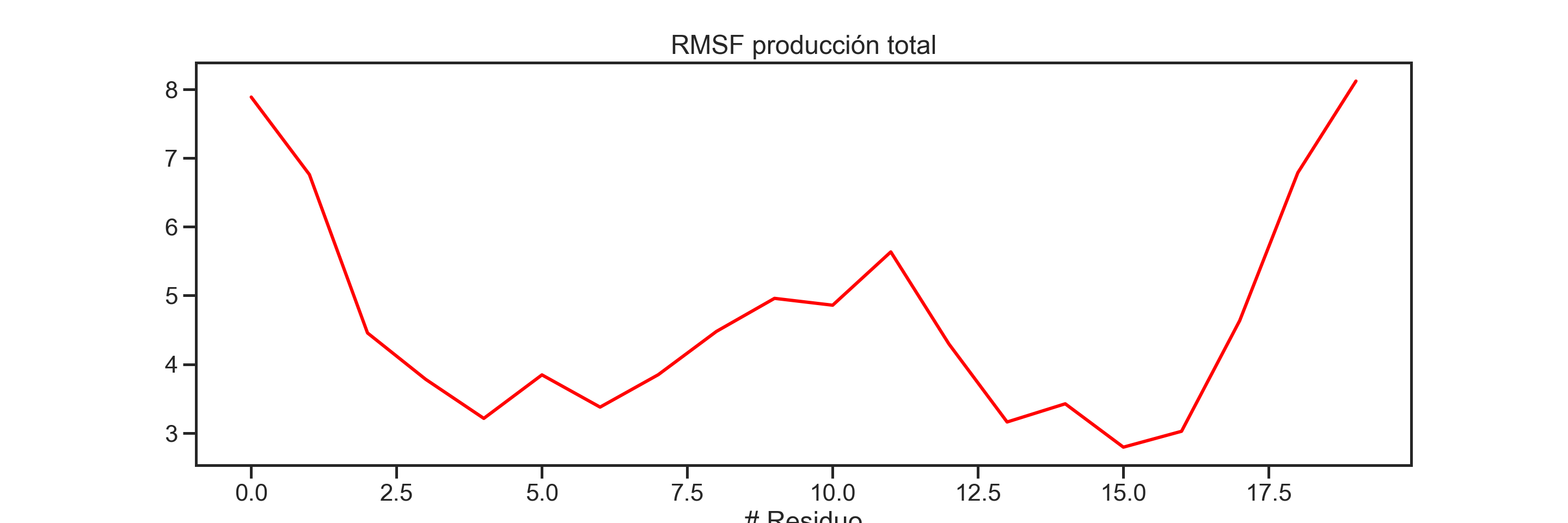
PAra terminar esta sección, un análisis interesante sería ver cómo el RMSF de la proteína va cambiando tomando ciertos intervalos de la producción.

Graficamos usando seaborn.

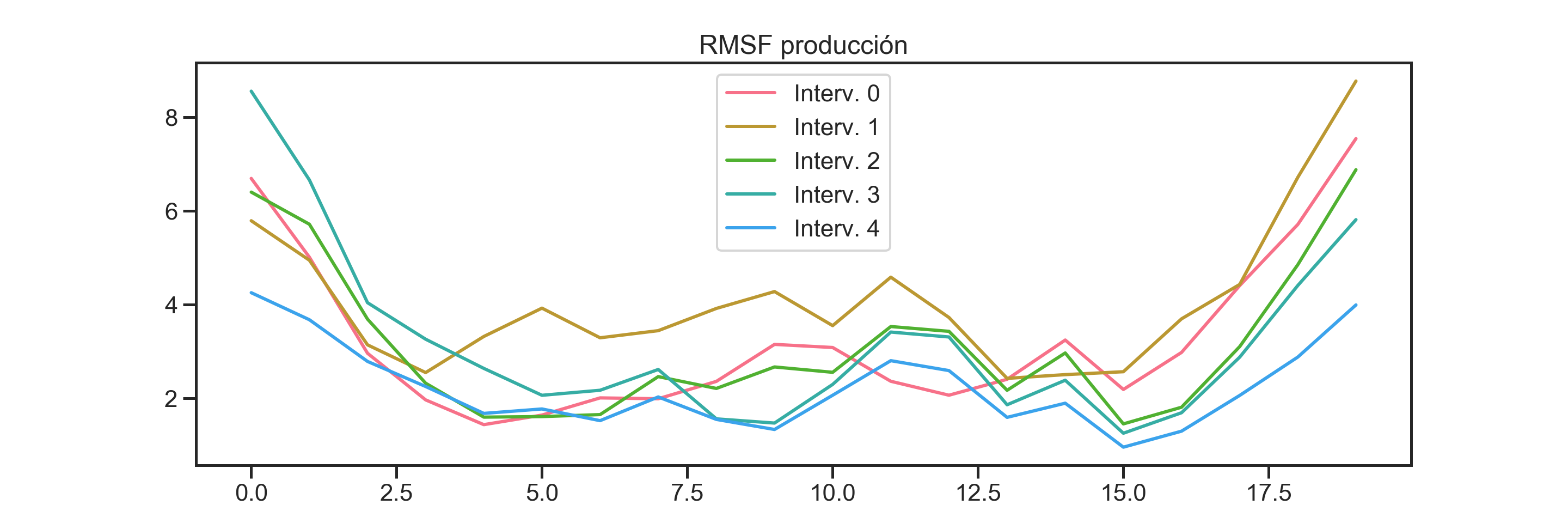
En general, podremos observar que hacia la última parte de la trayectoria, el backbone de la proteína tiende a ser más estable. Continuaremos con más análisis de la trayectoria en la siguiente sección.